1. Introduction

zk-Snark now is now be discussed by many people, however, few people understand what is the zk-Snark and how does it works. Just before the Christmas, I was lucky to have time to understand the whole picture of zk-Snark. If you find any mistake, I appreciate that you could tell me and also teach me:)

In this post, I would like to explain what is zk-snark, what problems does zk-snark try to solve. How to build a zk-snark system from the scratch.

The reading materials that related with this post is at:

[1] Exploring Elliptic Curve Pairings: https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627

[2] Quadratic Arithmetic Programs: from Zero to Hero: https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649

[3] zk-snark explained_basic_principles: https://blog.coinfabrik.com/wp-content/uploads/2017/03/zkSNARK-explained_basic_principles.pdf

[4] Pinocchio: Nearly Practical Verifiable Computation: https://eprint.iacr.org/2013/279.pdf

[5] Quadratic Span Programs and Succinct NIZKs without PCPs https://eprint.iacr.org/2012/215.pdf

[6] Zerocash: Decentralized Anonymous Payments from Bitcoinhttp://zerocash-project.org/media/pdf/zerocash-extended-20140518.pdf

[7] zk-snark in a nutshell: https://blog.ethereum.org/2016/12/05/zksnarks-in-a-nutshell/

[8] Bilinear mapping: https://www.encyclopediaofmath.org/index.php/Bilinear_mapping

Before you start, It is better to have the background knowledge about the elliptic curve pairing, homomorphic encryption, basic matrix operations, Bilinear mapping, zero knowledge proof.

if you have already familiar with the knowledge mentioned above, believe me, it is easy for you to understand the zk-snark:)

2. What is zk-snark Roughly speaking, zk-snark is one of Verifiable Computation protocol. It enables the verifier to prove that he/she knows the value and the polynomial without leaking any information about the value or the polynomial. This is of critical importance of privacy protection of the blockchain systems. One of the example is described as the follows:

• A customer purchases the item from the retailer.
• He/she pays the retailer through blockchain.
• To make his payment valid, he should proof that 1. he has enough balance to finish this payment. 2. he has paid the retailer enough money.
• However, none of the customer or the retail can leak any information about the price of this product, or how does this transaction be calculated.

Additionally, we would like to have the following features:

• This proof to be succinct to be easy to send to the network.
• It is easy for the verifier to verify.
• It should be non-interactive, which means that there should be no interaction between the prover and the verifier.

So, the zk-snark has the following features 7

• Succinct: The sizes of the messages are tiny in comparison to the length of the actual computation.

• Non-interactive: There is no or only little interaction. For zk-snark, there is usually a setup phase and after that a single message from the prover to the verifier. Furthermore, SNARKs often have the so-called “public verifier” property meaning that anyone can verify without interacting anew, which is important for blockchains.

• ARguments: The verifier is only protected against computationally limited provers. Provers with enough computational power can create proofs/arguments about wrong statements (Note that with enough computational power, any public-key encryption can be broken). This is also called “computational soundness”, as opposed to “perfect soundness”.

• of Knowledge: It is not possible for the prover to construct a proof/argument without knowing a certain so-called witness (for example the address she wants to spend from, the preimage of a hash function or the path to a certain Merkle-tree node).

3. How to build a zk-snark system

To explain the zk-snark as clear as I could, I will discuss it in two parts, for the first part, I will explain how to construct a QAP from the given polynomial. For the second part, I will explain how to use the arguments from QAP to construct the zk-snark.

3.1 Constructing the QAP

Before we touch any cryptographic stuff, I believe I should explain how to convert the polynomial to a QAP(t Quadratic Arithmetic Programs). I borrow the example in [2] to show how to do that.

Let’s say we have a polynomial $a^3+a+5=b$, and we want to show the verifier that we know there is a point (3,35) that satisfies this polynomial. What we do here is :

• 1. Algebraic Circuit
• 1. R1CS
• 1. QAP
• 1. Linear PCPs
• 1. Linear Interactive proofs
• 1. zk-Snark

So, firstly, we covert this polynomial into a Circuit.

<div align=center>

</div> let’s define the variables as follows:

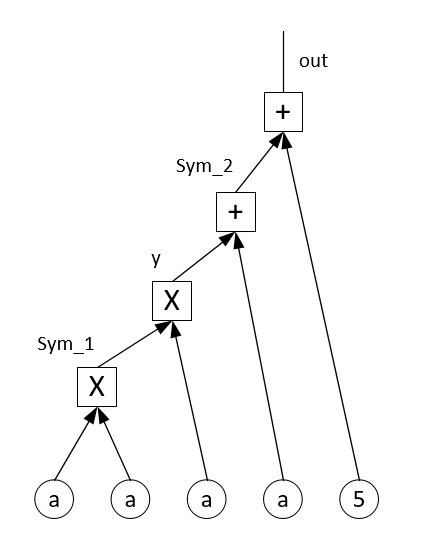
• ‘one’: The dummy value, it used to multiplied by the constant value.
• ‘x’: The input value.
• ‘out’: final output.
• ‘sym_1’: intermediate value.
• ‘smy_2’: intermediate value.
• ‘y’: intermediate value.

Let’s define g_l as the value enter the gate from left hand side, g_r as the value enter the gate from right hand side, and c as the output from the given gate. So for passing the first gate, the g_l, g_r and c are:

$$\begin{matrix} 'one' & 'x' & 'out' & 'sym_1' & 'y' &'sym_2' \\ 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \tag{1}$$

---